Evaluate an expression 41 Multiply (zx)3 by (zx) The rule says To multiply exponential expressions which have the same base, add up their exponents In our case, the common base is (zx) and the exponents are 3 and 1 , as (zx) is the same number as (zx)1 The product is therefore, (zx)(31) = (zx)4Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!Define a function T R 3 → R 2 by T (x, y, z) = (x y z, x 2y − 3z) (a) Show that T is a linear transformation (b) Find all vectors in the kernel of T (c) Show that T is onto (d) Find the matrix representation of T relative to the standard basis of R 3 and R 2 2) Show that B = { (1, 1, 1), (1, 1, 0), (0, 1, 1)} is a basis for R 3

If X Y Z 0 Show That X 3 Y 3 Z 3 3xyz With Video
Prove that (x-y)^3 (y-z)^3 (z-x)^3=3(x-y)(y-z)(z-x)
Prove that (x-y)^3 (y-z)^3 (z-x)^3=3(x-y)(y-z)(z-x)-1 Which of the subsets of R 3 is a subspace of R 3 a) W = {(x,y,z) x y z = 0} b) W = {(x,y,z) x y z = 1} I was wondering if my answer for A is correct Homework Equations 3 A) W = {(x,y,z) x y z = 0} Since, x y z = 0 Then, the values for all the variables have to be zero Therefore, the only vector in W is the zero vectorSuch that there exists a vector x with Ax = bThus we have the following Theorem Let A be an m×n matrix Define TRn 6 Rm by, for any x in Rn, T(x) = AxThen T is a linear transformation Furthermore, the kernel of T is the null space of A and the range of T is the column



Using Properties Of Determinants Prove That 3x X Y X Z X Y 3y Z Y X Z Y Z 3z 3 X Y Z Xy Yz Zx Sarthaks Econnect Largest Online Education Community
Example 32 Show that Determinant = 2xyz (x y z)^3 Class 12 Example 32Show that Δ = 8((𝑦𝑧)2&𝑥𝑦&𝑧𝑥@𝑥𝑦&(𝑥𝑧)2&𝑦𝑧@𝑥𝑧&𝑦𝑧&(𝑥𝑦)2) = 2xyz (x y z)3 Solving LHS Δ =Xyz = x y z 2 Add 1 (zx zy xy) (x y z) to both sides xyz 1 (zx zy xy) (x y z) = 2x 2y 2z 3 zx zy xy Rearrange the terms on both sides 1 x y xy z zx zy xyz = 1 y z yz 1 x z zx 1 x y xyAre continuous on R3, so f is differentiable on R3 • Explicitly, we write f = (f1,f2) where f1,f2 R3 → Rare given by f1(x,y,z) = x2 yz, f2(x,y,z) = sin(xyz)z The partial derivatives are ∂f1 ∂x (x,y,z) = 2x, ∂f1 ∂y (x,y,z) = z, ∂f1 ∂z (x,y,z) = y, ∂f2 ∂x (x,y,z) = yzcos(xyz), ∂f2 ∂y (x,y,z) = xzcos(xyz), ∂f3 ∂z
Simple and best practice solution for y=xz/3 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand,3 system shown below Enter the values of x, y, and z X 2y – z = –3 (1) 2x – y z = 5 (2) x Get the answers you need, now!Z of rational numbers by taking x = 2/3, y = 4/6, z = 7/9 Welcome to Sarthaks eConnect A unique platform where students can interact with teachers/experts/students to get solutions to their queries
A= (abc)^3 (abc)^3 (bca)^3 (cab)^3 chia hết cho 24 Thanks for your help ^^ Trở lên trên(y z) = x ×We know the corollary if abc = 0 then a3 b3 c3 = 3abcUsing the above identity taking a = x−y, b = y−z and c= z−x, we have abc= x−yy−zz −x= 0 then the equation (x− y)3 (y−z)3 (z−x)3 can be factorised as follows(x−y)3 (y−z)3 (z−x)3 = 3(x−y)(y−z)(z−x)Hence, (x−y)3 (y−z)3 (z −x)3 = 3(x−y)(y −z)(z −x)




Satyabama Niversity Questions In Vector




Without Finding The Cubes Factorise X Y Y Z Z X Brainly In
Y x ×If the polynomial k 2 x 3 − kx 2 3kx k is exactly divisible by (x3) then the positive value of k is ____Taking 2 common from R 1, we get LHS = `2 (x y z, x y z, x y z), (z x, x y, y x), (y z, z x, x y)` Applying R 1 → R 1 – R 3, we get LHS = `2 (x, y, z), (z x, x y, y x), (y z, z x, x y)` Applying R 2 → R 2 – R 1, we get




X Y 3 Y Z 3 Z X 3 Novocom Top




X3 Y3 Z3 3xyz X Y Z X2 Y2 Z2 Xy Yz Zx Proof It Lhs To Rhs Brainly In
先将等式分解成y=y (z/x) z之后表达式 (z)的值为3,z的值为2 x之后表达式 (x)的值为2,x的值为2 之后 (z/x)的值为1 (如果java中,则int型,会被取整,如果不取整,这里就是15),再执行y (z/x)=3(如果不取整就是35); Systemoutprintln (y);This is the Solution of Question From RD SHARMA book of CLASS 9 CHAPTER POLYNOMIALS This Question is also available in R S AGGARWAL book of CLASS 9 You can FAnswer x3 y3 z3 −3xyz = (xyz)(x2 y2 z2 −xy−yz−zx) First take LHS (xyz)(x2 y2 z2 −xy−yz−zx) To multiply two polynomials, we multiply each monomial of one polynomial (with its sign) by each monomial (with its sign) of the other polynomial




Prove That 1 X Yz 1 Y Zx 1 Z Xy X Y Y Z Z X




If X Y Z 0 Show That X 3 Y 3 Z 3 3xyz With Video
Find the value of X, Y and Z calculator to solve the 3 unknown variables X, Y and Z in a set of 3 equations Each equation has containing the unknown variables X, Y and Z This 3 equations 3 unknown variables solver computes the output value of the variables X and Y with respect to the input values of X, Y and Z coefficientsI collected a solution Need to prove x 2 y 2 z 2 5 x y z and does not require problemspecific tricks We want to calculate bounds for the function f=x y y z z x x y z\ , Here's a straightforward way, which is not very elegant, 6 9 9 ∗ 5 3 3 MatrixXyz=6, 2xyz=3, 3xz=0 \square!




X Y 3 Y Z 3 Z X 3 Factorise Novocom Top




Using Properties Of Determinant Prove That 1 X Y X 2 Y 2 1
The answer is yes, the rational points on your surface lie dense in the real topology Let's consider the projective surface S over Q given by X 3 Y 3 Z 3 − 3 X Y Z − W 3 = 0 It contains your surface as an open subset, so to answer your question we might as well show that S ( Q) is dense in S ( R) Observe that S has a singularTrả lời (1) • V T =(xyz)3−x3−y3−z3 V T = ( x y z) 3 − x 3 − y 3 − z 3 = (xy)33z(xy)2 3(xy)z2z3−x3−y3−z3 = ( x y) 3 3 z ( x y) 2 3 ( x y) z 2 z 3 − x 3 − y 3 − z 3 = x33x2y3xy2y33z(xy)2 3xz2 3yz2−x3 −y3 = x 3 3 x 2 y 3 x y 2 y 3 3 z ( x y) 2 3 x z 2 3 y z 2 − x 3 − y 3Equations Tiger Algebra gives you not only the answers, but also the complete step by step method for solving your equations 3*3x*y*4z*x*y*z so that you understand better
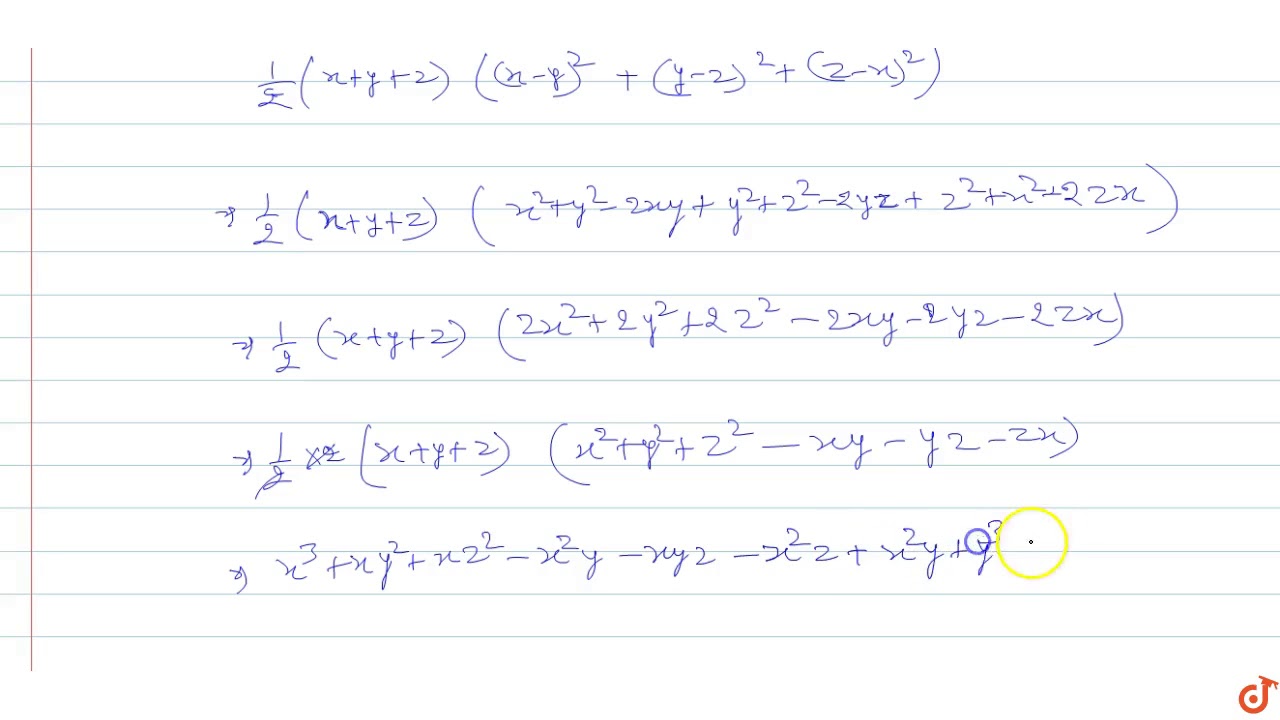



Verify That X 3 Y 3 Z 3 3xyz 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Youtube



Using The Properties Of Determinants Y2z2 Yz Y Z Z2x2 Zx Z X X2y2 Xy X Y 0 Studyrankersonline
Find an answer to your question prove (xy)³The question given is Show that $(xyz)^3(yzx)^3(zxy)^3(xyz)^3=24xyz$ What I tried is suppose $a=(yzx),\ b=(zxy)$ and $c=(xyz)$ and then noted that $abc=xyz$ So the questXyz =0we know thatx3 y3 z3 −3xyz = (xyz)(x2 y2 z2 −xy−yz−zx)then⇒ x3 y3 z3 −3xyz = 0⇒ x3 y3 z3 = 3xyz




Ex 4 2 9 Show That X X2 Yz Y Y2 Zx Z Z2 Xy X Y Y Z




Prove X Y 3 Y Z 3 Z X 3 3 X Y Y Z Z X Brainly In
3 Curl The curl of a vector field, F(x,y,z), in three dimensions may be written curlF(x,y,z) = ∇×F(x,y,z), ie ∇×F(x,y,z) = (∂F 3 ∂y − ∂F 2 ∂z)i−(∂F 3 ∂x − ∂F 1 ∂z)j (∂F 2 ∂x − ∂F 1 ∂y)k = i j k ∂ ∂x ∂ ∂y ∂ ∂z F 1 F 2 F 3 It is obtained by taking the vector product of the vector operatorVerify the property x ×To ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW Verify that `x^3y^3z^33x y z=1/2(xyz)(xy)^2(yz)^2(zx)^2`




Find The Value Of X Y Y Z Z X Brainly In




The Value Of X Y 3 Y Z 3 Z X 3 X 2 Y 2 3 Y 2 Z 2
Chứng minh rằng với mọi a,b,c thuộc Z thìAlgebracalculator x2yz=0, 2xyz=1, 3xy2z=5 en Related Symbolab blog posts Middle School Math Solutions – Inequalities Calculator Next up in our Getting Started maths solutions series is help with another middle school algebra topic solvingSimplificar (xyz)(xyz) Expanda multiplicando cada término de la primera expresión por cada término de la segunda expresión Simplifica los términos Toca para ver más pasos Combine the opposite terms in Toca para ver más pasos Reorder the factors in the terms and Sumar y




Prove That 1 1 1 X Y Z X 3 Y 3 Z 3 X Y Y Z




Ex 4 2 9 Show That X X2 Yz Y Y2 Zx Z Z2 Xy X Y Y Z
Transcript Ex 25, 13 If x y z = 0, show that x3 y3 z3 = 3xyz We know that x3 y3 z3 3xyz = (x y z) (x2 y2 z2 xy yz zx) Putting x y z = 0, x3 y3 z3 3xyz = (0) (x2 y2 z2 xy yz zx) x3 y3 z3 3xyz = 0 x3 y3 z3 = 3xyz Hence provedWhat must be subtracted from 4x^42x^36x^22x6 so that the result is exactly divisible by 2x^2x1?If x1/x=5,then find value of x^31/x^3 The valuesof 249square 248square is 729X3512y3 Factorise (abc)³a³b³c3 I need very urgently please answer as quickly as you can Experts, please help me with the following questions attached below in the image Questions are from chapter POLYNOMIALS, grade 9 (please answer all of them




X 3 Y Z 3 Y 3 Z X 3 Z 3 X Y 3 Youtube




Prove That X Y 3 Y Z 3 Z X 3 3 X Y Y Z Z X 0
Rewrite the expression x y z = 3 ⋅ a x y z = 3 ⋅ a xy z = 3a x y z = 3 a Move all terms not containing y y to the right side of the equation Tap for more steps Subtract x x from both sides of the equation y z = 3 a − x y z = 3 a x Subtract z z from both sides of the equation y = 3 a − x − z y = 3 a x zExplanation Given, y/ (x z) = (y x)/z = x/y y z = x y x 2 y z x z ( 1) Also x y = y x z ⇒ x 2 x z = y 2 ( 2) Using (1) and (2), we get yz = xy yz y 2 2yz = xy y 2 2z = x y3(xy) (yz( z x)= 12x³




The Value Of X Y 3 Y Z 3 Z X 3 9 X Y Y Z Z X Is




X 3 Y 3 Z 3 3xyz X Y Z X 2 Y 2 Z 2 Xy Yz Zx A 3 B 3 C 3 3abc A B C A 2 B 2 C 2 Ab Ca Youtube
(B∪C) Obviously, x belongs to A and y belongs to (B∪C) x∈A and y∈ (B∪C) x∈A and (y∈B or y∈C)Solve the 3 ×33 3 3 3 uu ux y z xy yz zx xy zxyz xyz ∂∂∂−−− = ∂∂∂ − or ()() 22 2 22 2 uu u3x y z xy yz zx xy zx y z x y z xy yz zx ∂∂∂−−− ∂∂∂ = − −− ⇒ () uuu 3 xy zxyz ∂∂∂ = ∂∂∂ (5) or U = 3(x y z)–1 Likewise, obtain partial derivatives of expression (5) with respect to x



Using Properties Of Determinants Prove The Following X X 2 1 Px 3 Y Y 2 1 Py 3 Z Z 2 1 Pz 3 1 Pxyz X Y Y Z Z X Sarthaks Econnect Largest Online Education Community



Using Properties Of Determinants Prove That Y X 2 Xy Zx Xy X Z 2 Yz Xz Yz X Y 2 2xyz X Y Z 3 Sarthaks Econnect Largest Online Education Community
Prove that (xy)3 (yz)3 (zx)3 3(xy) (yz) (zx)= 2(x3y3z33xyz) Maths PolynomialsDet ( x y z y z x z x y) = 3 x y z − ( x 3 y 3 z 3) Let AMGM n stands for the statement of the arithmeticgeometric inequality in n variables A classical, elementary approach (due to Cauchy, Cours d'Analyse) is to show AMGM 2 ⊢ AMGM 4 ⊢ AMGM 3Associativity of addition Addition and multiplication are both associative operations (x y) z = x (y z) for all x, y and z (x * y) * z = x * (y * z) for all x, y and z Notice that subtraction and division are not associative operations (x y) z != x (y z) (except when z = 0) (x y) z != x (y z) (except when x = 0 or z = 1)




Using Properties Of Determinants Prove The Following 3x X Y X Z X Y 3y Z Y X Z Y Z 3z 3 X Y Z Xy Yz Xz




If X Y Z 6 And Xy Yz Zx 11 And Xyz 6 Is Given Find The Valu
Writing any polynomial directly just requires listing all possible exponent combinations of a^x*b^y*c^z where every term has xyz=3 and the coefficient of each term is (xyz)!/ (x!y!z!) This works for any length polynomial and in this case we would have a^3 b^3Giới tính Nữ ĐãGửi 2217 C/m (xyz)^3 x^3 y^3z^3 = 3 (xy) (yz) (zx) Từ đó



Using Properties Of Determinants Prove That 3x X Y X Z X Y 3y Z Y X Z Y Z 3z 3 X Y Z Xy Yz Zx Sarthaks Econnect Largest Online Education Community



If X Y 3 Y Z 3 Z X 3 15 How Do I Find The Value Of X Y Y Z Z X Quora
Answer answered Prove that 2x^32y^32z^36xyz= ( (xyz) { (xy)^2 (yz)^2 (zx)^2} hence evaluate 2 (13)^32 (14)^32 (15)^36*13*14*15 Plz give the answer in detailPlz solve thisThe best answer will be marked as brainliest 2 See answers report flag outlined bell outlined Log in to add commentIf X 3 X − Y − Z = Y 3 Y − Z − X = Z 3 Z − X − Y and X Y Z ≠ 0 Then Show that the Value of Each Ratio is Equal to 1First, subtract $3xyz$ from both sides of the equation $$x^3y^3z^3=3(xyzxyz) \\ x^3y^3z^33xyz = 3(xyz)$$ Now, using this factorisation, observe $$ (xyz)(x^2y^2z^2xyyzzx)=3(xyz)$$ Since $x,y$, and $z$ are positive integers which implies $xyz\neq 0$, you can divide the equation by $xyz$ to get $$ x^2y^2z^2 xyyzzx = 3$$ Now, from the above equation, it's easy to observe that $$(xy)^2(yz)^2(zx



If 1 X 1 Y 1 Z 0 And X Y Z 9 Then What Is The Value Of X 3 Y 3 Z 3 3xyz Quora



Using The Properties Deteminants 3x X Y X Z X Y 3y Z Y X Z Y Z 3z Studyrankersonline
Swagat Swargari answered this Using identity a 3 b 3 c 3 3abc = (abc) (a 2 b 2 c 2 ab bc ca) (xy) 3 (yz) 3 (zx) 3 3 (xy) (yz) (zx) = (xy yz zx) (xy) 2 (yz) 2 (zx) 2 (xy) (yz) (yz) (zx) (zx) (xy)Piyush Balwani@ piyushbalwani 0113 am I can tell you the formal proof,but without venn diagram (x,y)is all elements that belongs to A×If you want three Rational numbers x , y, z satisfying x^ 3 y^ 3 z ^3 =33 then there are still infinitely many, though they are somewhat harder to find If you want three Integers, or whole numbers, satisfying that equation, then you'll need to be patient nobody knows if such three numbers exist 33 33 is the smallest natural number for which it is unknown if it can b




X Y 3 Y Z 3 Z X 3 3 X Y Y Z Z X 2 X3 Y3 Z3 3xyz Mathematics Topperlearning Com T86qex55




If X Y Z And X X 3 X 4 1 Y Y 3 Y 4 1 Z Z 3 Z 4 1 0 Prove That Xyz Xy Yz Zx X Y Z
(xy)^3 (yz)3 (zx)^3 >= 3(xy)(yz)(zx) But that is not the question set Please note that this is the first chapter and all that has been covered is basic number theory, rational powers, inequalities and divisibility I am assuming those are the only tools I have at my disposal, I have not been introduced to any identities etcTaking x y z common from the first row, we get `=(xyz)1,1,1,2z,2z,zxy,xyz,2x,2x` Now, applying C 2 → C 2 − C 1 and C 3 → C 3 − C 1 , we get




Factorise 2x Y Z 3 2y Z X 3 2z X Y 3 Brainly In




X Y Xy 3 Y Z Yz 8 And Z X Zx 15 What Is The Value Of 6xyz Brainly In




X Y 3 Y Z 3 Z X 3 Novocom Top



Using Properties Of Determinants Prove That 3x X Y X Z X Y 3y Z Y X Z Y Z 3z 3 X Y Z Xy Yz Zx Sarthaks Econnect Largest Online Education Community



What Is The Unit Normal To The Surface Xy Yz Zx 3 Of The Point 1 1 1 Quora




X Y 3 Y Z 3 Z X 3 Novocom Top




X Y 3 Y Z 3 Z X 3 Novocom Top




If Math X Y Z 0 Math Then Math X Y Z 3 Y Z X 3 Z X Y 3 Math Quora




Prove X Y 3 Y Z 3 Z X 3 3 X Y Y Z Z X Brainly In



Using Properties Of Determinants Prove That X Y Z X 2 Y 2 Z 2 X 3 Y 3 Z 3 Xyz X Y Y Z Z X Sarthaks Econnect Largest Online Education Community
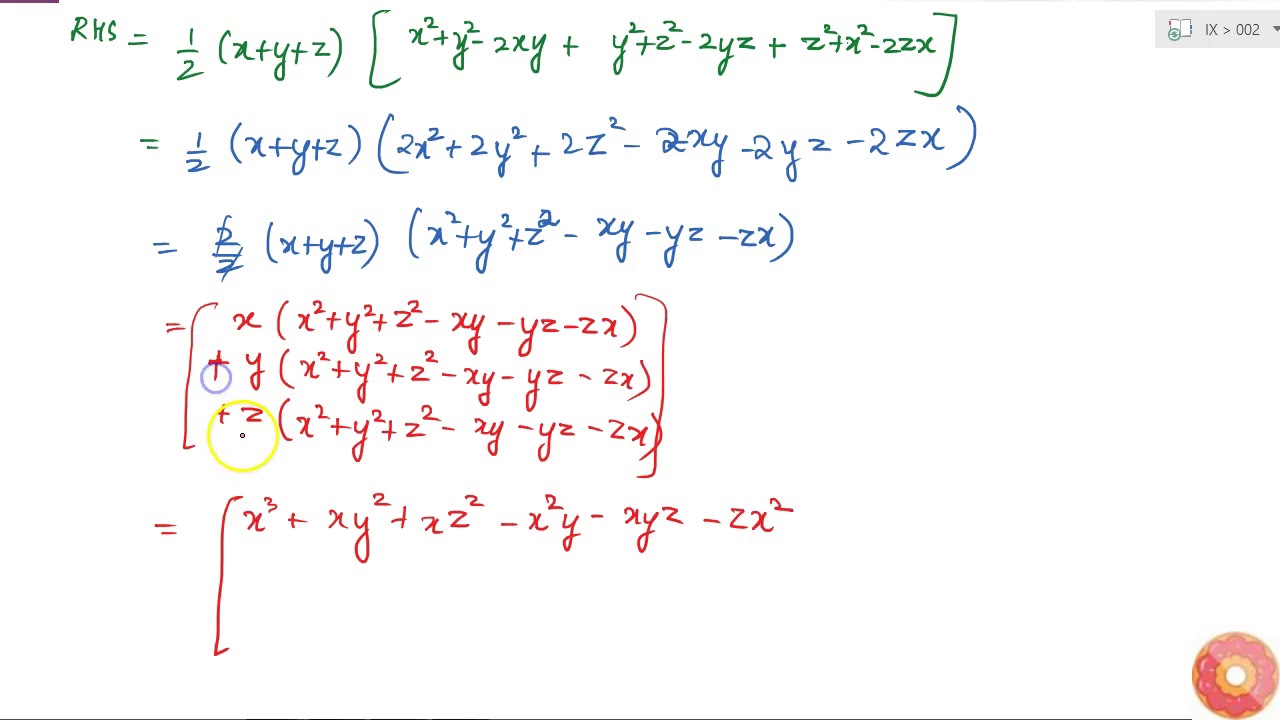



Verify That X 3 Y 3 Z 3 3x Y Z 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Youtube




Is 8 X 3 Y 3 Z 3 2 Ge 9 X 2 Yz Y 2 Xz Z 2 Xy True For Nonnegative Numbers Mathematics Stack Exchange




Prove That X Y Y Z Z X 3 X Y Y Z Z Y 2 X Y Z 3xyz Brainly In




Verify That X3 Y3 Z3 3xyz 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Brainly In




Using Properties Of Determinant Prove That 3x X Y X Z X Y 3y Z Y X Z Y Z 3 Youtube



What Is The Value Of X Y Z Where Xyz Xy Xz Yz X Y Z 3 Quora



Prove That 2x3 2y3 2z3 6xyz X Y Z X Y 2 Y Z 2 Z X 2 Hence Evaluate 2 7 3 2 9 3 2 13 3 6 7 9 13 Mathematics Topperlearning Com V780o2jj




The Value Of X Y 3 Y Z 3 Z X 3 9 X Y Y Z Z X Is Equal To A 0 B 1 9 C 1 3 D 1 Youtube




X Y 3 Y Z 3 Z X 3 Novocom Top
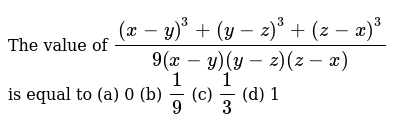



The Value Of X Y 3 Y Z 3 Z X 3 9 X Y Y Z Z X Is




X 3 Y 3 3 Y 3 Z 3 3 Z 3 X 3 3 X Y 3 Y Z 3 Z X 3 Youtube




Solve 1 Xy Xy X Y 1 Yz Yz Y Z 1 Zx Zx 2 X



Using The Properties Of Determinants Y2z2 Yz Y Z Z2x2 Zx Z X X2y2 Xy X Y 0 Studyrankersonline



Using The Properties Deteminants 3x X Y X Z X Y 3y Z Y X Z Y Z 3z Studyrankersonline



If X Y And Z Are Real Numbers Such That X Y Z 5 And Xy Yz Zx 3 Then What Is The Largest Value That X Can Have Quora




Evaluate Please X 2 Y 2 3 Y 2 Z 2 3 Z 2 X 2 3 Divided By X Y 3 Y Z 3 Z X 3 Brainly In



If Math X Y Z 0 Math How Do You Prove That Math X 3 Y 3 Z 3 3xyz Math Quora




If Xy 3 Yz 6 Zx 2 Find X Y Z Brainly In



Using Properties Of Determinants Prove The Following X X 2 1 Px 3 Y Y 2 1 Py 3 Z Z 2 1 Pz 3 1 Pxyz X Y Y Z Z X Sarthaks Econnect Largest Online Education Community




X Y 3 Y Z 3 Z X 3 Factorise Novocom Top




If X Y Z 6 And Xy Yz Zx 11 And Xyz 6 Is Given Find The Value Of X 3 Y 3 Z 3 Youtube
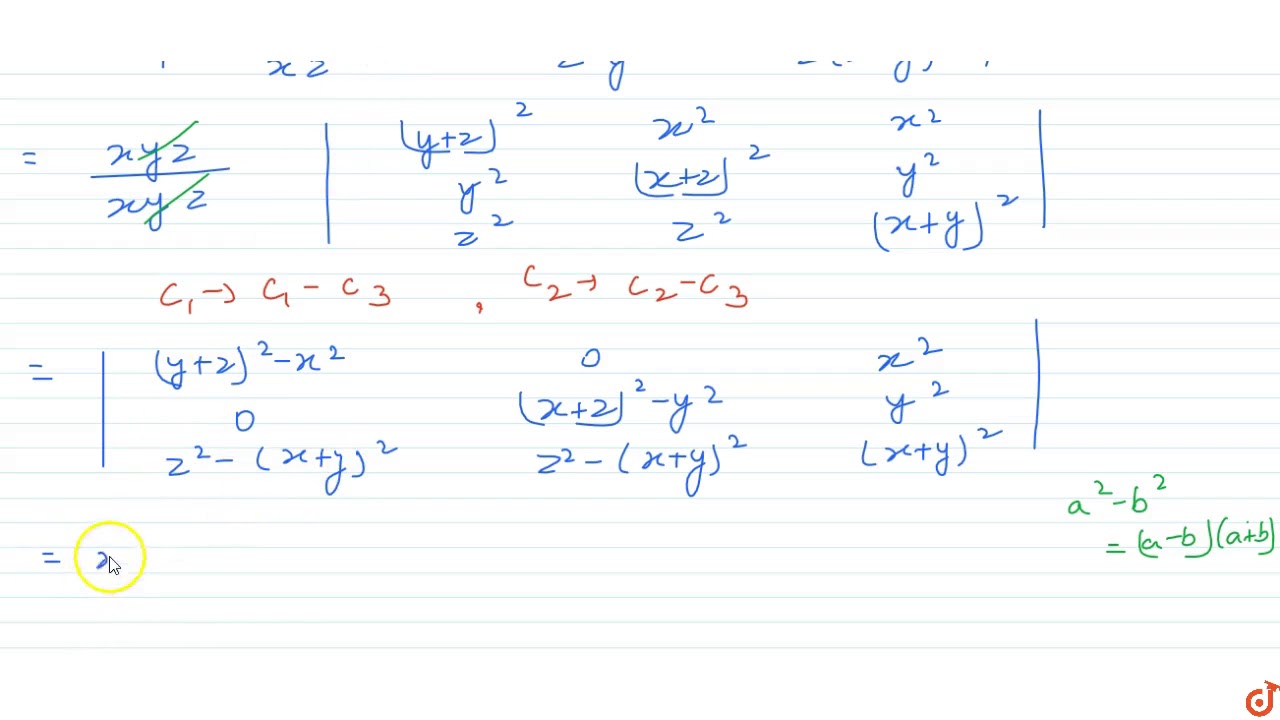



Prove That Y Z 2 Xy Zx Xy X Z 2 Yz Xz Zy X Y 2 Xyz X Y Z 3 Youtube



If X Y Z 6 And Xy Yz Zx 10 Then What Is The Solution Of X 3 Y 3 3xyz Quora
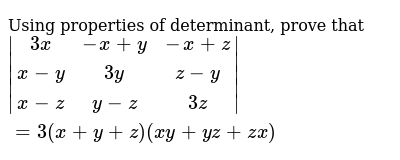



Using Properties Of Determinant Prove That 3x X Y X Z




1 Using Properties Of Determinants Prove The Following X Y Z X2 Y2 Z2 X3 Y3 Z3 Maths Determinants Meritnation Com



Using Properties O Determinants Prove That 1 X X 3 1 Y Y 3 1 Z Z 3 Sarthaks Econnect Largest Online Education Community



Using Properties Of Determinants Prove That Y X 2 Xy Zx Xy X Z 2 Yz Xz Yz X Y 2 2xyz X Y Z 3 Sarthaks Econnect Largest Online Education Community




Prove X Y 3 Y Z 3 Z X 3 3 X Y Y Z Z X Brainly In




Ex 4 2 9 Show That X X2 Yz Y Y2 Zx Z Z2 Xy X Y Y Z
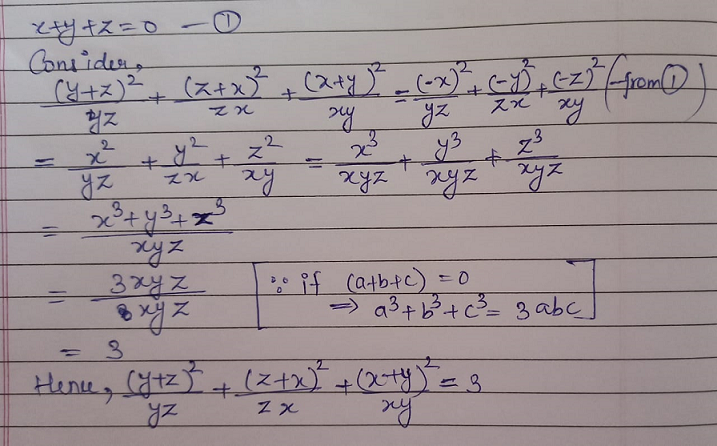



How To Solve If X Y Z 0 Find The Value Of Y Z 2 Yz Z X 2 Zx X Y 2 Xy Mathematics Topperlearning Com 7bcu50oo




Ex 2 5 12 Verify That X3 Y3 Z3 3xyz 1 2 Ex 2 5




X3 Y3 Z3 3xyz 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Novocom Top




How To Factorise Using The Identity X3 Y3 Z3 3xyz X Y Z X2 Y2 Z2 Xy Yz Zx Youtube




The Value Of X Y 3 Y Z 3 Z X 3 9 X Y Y Z Z X Is



Suppose That X Y And Z Are Positive Integers Such That Xy 6 Xz 10 And Yz 15 What Is The Value Of Xyz Quora




12 Expansion Of X Y 3 Y Z 3 Z X 3 Is A 2x 3 2y




Prove That X Y 3 Y Z 3 Z X 3 3 X Y Y Z Z X Maths Polynomials Meritnation Com




Prove That X Y Y Z Z X 3 X Y Y Z Z Y 2 X Y Z 3xyz Brainly In




Factorize X Y 3 Y Z 3 Z X 3 Youtube



Using Properties Of Determinants Prove That X 2 1 Xy Xz Xy Y 2 1 Yz Xz Yz Z 2 1 1 X 2 Y 2 Z 2 Sarthaks Econnect Largest Online Education Community




If Math X Y Z 0 Math What Is The Value Of Math Frac X 2 Yz Frac Y 2 Zx Frac Z 2 Xy Math Quora



How To Factorize X Y Y Z Z X Quora




X Y 3 Y Z 3 Z X 3 Novocom Top




Prove That 2x 3 2y 3 2z 3 6xyz X Y Z X Y 2 Y Z 2 Z X 2 Brainly In




Using Properties Of Determinant Prove That 3x X Y X Z




Vector
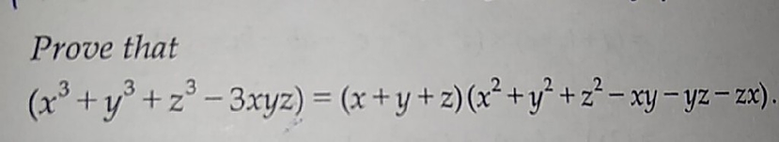



X 3 Y 3 Z 3 3 X Y Z X Y Scholr



Services Artofproblemsolving Com Download Php Id Yxr0ywnobwvudhmvzs8xl2u2m2vizddlyjk1zgm4m2ixmdqzotc2zdq5ndhmmdy3m2fiztfk Rn Vxnlznvsiefsz2vicmfpyybnyw5pchvsyxrpb25zlnbkzg




If Math X Y Z 0 Math Then Math X Y Z 3 Y Z X 3 Z X Y 3 Math Quora




Question Bank Abcabc 2 2 5 aa 4 Pdf X Y Y Z Z X Xy Yz Zx X Y Y Z Z X 1 A



If Math X Y Z 0 Math How Do You Prove That Math X 3 Y 3 Z 3 3xyz Math Quora




Without Expending Prove That I B 2 C 2 B C




X Y Z 3 Y Z X 3 Z X Y 3 X Y Z 3 24xyz Mathematics Stack Exchange




The Value Of X Y 3 Y Z 3 Z X 3 9 X Y Y Z Z X Brainly In



Www Topperlearning Com Answer Using Identities Prove That X Y Z 2 3 Xy Yz Zx Where X Y Z Are Positive Real Numbers 3gc3fduu




X Y 3 Y Z 3 Z X 3 Novocom Top




If X Y Z 9 And Xy Yz Zx 23 The Value Of X 3 Y 3 Z 3 3xyz Youtube




Prove That X Y 3 Y Z 3 Z X 3 3 X Y Y Z Z X Novocom Top




Simplify X Y Z Y Z X Z X Y Z X Y X Y Z Y Z X If X Y Z 0 Youtube




Factorise X Y 3 Y Z 3 Z X 3 Brainly In



0 件のコメント:
コメントを投稿