The Pythagorean Identities Cool Math has free online cool math lessons, cool math games and fun math activities Really clear math lessons (prealgebra, algebra, precalculus), cool math games, online graphing calculators, geometry art, fractals, polyhedra, parents and teachers areas too/11/16 · These are called Pythagorean identities because they're just the good old Theorem of Pythagoras in new clothes Learn the really basic one, namely sin² A cos² A = 1, and the others are easy to derive from it in a single step Students seem to get bogged down in the huge number of trigonometric identities As I said earlier, I think the problem is that students are expected toQuadratic Trigonometric Identities https//wwwyoutubecom/watch?v=fTQaJ0Tw2_8&list=PLJma5dJyAqqlHeKCBFiWwve_12xt8Sz3
Derivatives Of Trigonometric Functions
Is tan^2x+1=secx a pythagorean identity
Is tan^2x+1=secx a pythagorean identity-The Pythagorean identity tells us that no matter what the value of θ is, sin²θcos²θ is equal to 1 We can prove this identity using the Pythagorean theorem in the unit circle with x²y²=1 Created by Sal Khan Google Classroom Facebook TwitterFree multiple angle identities list multiple angle identities by request stepbystep This website uses cookies to ensure you get the best experience By using this website, you agree to our Cookie Policy Learn more Accept Solutions Graphing Practice;



Understanding Pythagorean Identities Studypug
How to prove the pythagorean identities?Free math lessons and math homework help from basic math to algebra, geometry and beyond Students, teachers, parents, and everyone can find solutions to their math problems instantlyThe Pythagorean formula for sines and cosines This is probably the most important trig identity Identities expressing trig functions in terms of their complements There's not much to these Each of the six trig functions is equal to its cofunction evaluated at the complementary angle Periodicity of trig functions Sine, cosine, secant, and cosecant have period 2π while tangent and
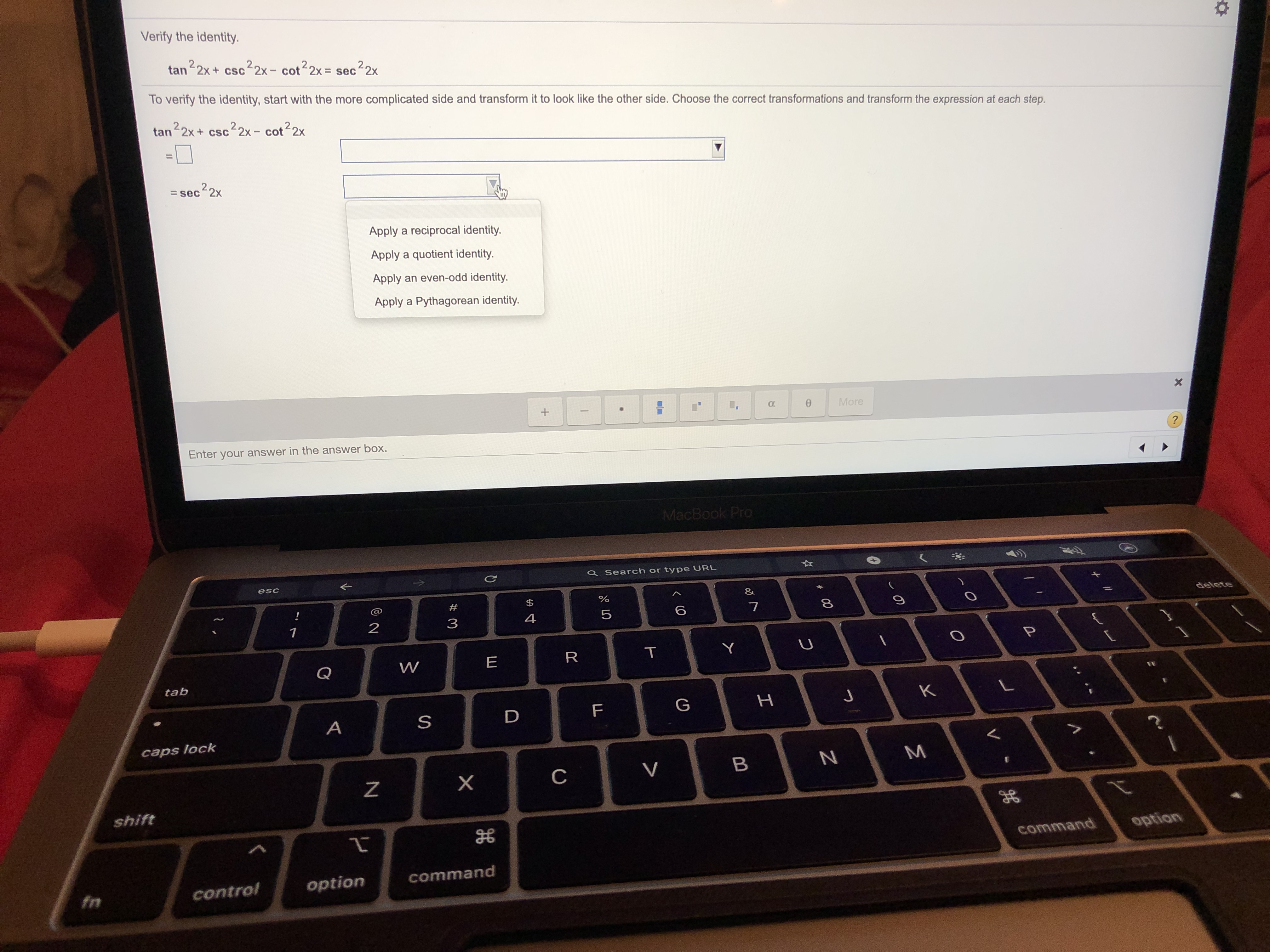
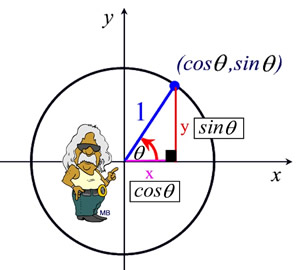
· Basic and Pythagorean Identities Note that the three identities above all involve squaring and the number 1 You can see the PythagoreanThereom relationship clearly if you consider the unit circle, where the angle is t, the "opposite" side is sin(t) = y, the "adjacent" side is cos(t) = x, and the hypotenuse is 1Question Verify the identity tan^2x sin^2x cos2x = sọc 2x To verify the identity, start with the more complicated side and transform it to look like the other side Choose the correct transformations and transform the expression at each step tan * sin 2x cos2x secx Factor out the greatest common factor Apply a Pythagorean identity to the sum of the second andTan is an "odd" identity quotient identity (for tangent) algebra/ simplify 1) 2) cos tan (x) Strategy 1) get rid of the negatives 2) üy to change terms to sin's and COS's 3) simplFy • tan (x) tan x sm x cos x smx cos (x) cosx • cosx • Prove Strategy
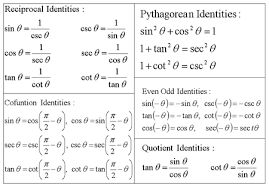
· Other Fundamental Trigonometric Identities Applying the Reciprocal Identities Here are some different important identities or formulas that can be used together with the reciprocal identities when simplifying or verifying identities Pythagorean Identities sin 2 (θ) cos 2 (θ) = 1 tan 2 (θ) 1 = sec 2 (θ) cot 2 (θ) 1 = csc 2 (θFormulas and Identities Tangent and Cotangent Identities sincos tancot cossin qq qq qq == Reciprocal Identities 11 cscsin sincsc 11 seccos cossec 11 cottan tancot qq qq qq qq qq qq == == == Pythagorean Identities 22 22 22 sincos1 tan1sec 1cotcsc qq qq qq = = = Even/Odd Formulas ( ) ( ) ( ) ( ) ( ) ( ) sinsincsccsc coscossecsec tantancotcotBy applying the Pythagorean identity and geometric proof methods, these definitions can readily be shown to coincide with the definitions of tangent, cotangent, secant and cosecant in terms of sine and cosine, that is = , = , = , = Trigonometric functions Sine, Cosine, Tangent, Cosecant (dotted), Secant (dotted), Cotangent (dotted) – animation Since a


Solved A First Rewrite The Left Hand Side 1 Tan 2x In Terms Of Sin X And Cos X B Next Add The Two Terms In The Expression You Got In Part
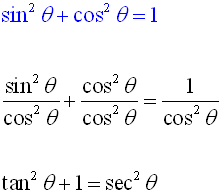


Pythagorean Identities Mathbitsnotebook Ccss Math
Pythagorean Trigonometric Identities We already are aware of one of the pythagorean trigonometric identities which is the definition of the unit circle such that (12) \begin{equation} cos^2x sin^2x = 1 \end{equation} However, there are other pythagorean trigonometric identities such as the following (13) \begin{align} 1^2 tan^2x = sec^2x \quad 1^2 cot^2x = csc^2x1 Pythagorean identities sin 2xcos x= 1 1tan2 x= sec2 x 2 SumDifference formulas sin(x y) = sinxcosy sinycosx cos(x y) = cosxcosy sinxsiny tan(x y) = tanx tany 1 tanxtany cot(x y) = cotxcoty 1 cotx coty arctan( ) arctan( ) = arctan 1 3 Double Angle formulas sin2x= 2sinxcosx cos2x= cos 2x sin2 x= 2cos x 1 = 1 2sin2 x tan2x= 2tanx 1 2tan xChoose the correct transformations and transform the expression at each step tan?zx sin 2x cos2x Factor out the greatest common factor Apply a Pythagorean identity to the sum of the second and third term Apply a Pythagorean identity to the sum of the first and second term Express in terms of sines and cosines Verify the identity tan 2x sin 2x cos2x = secx To verify



Show That The Following Are Not Trigonometric Identities 1 Tan 2x 2tan X 2 Sec X Sqrt 1 Tan 2 X 3 Sin X Y Sin X Sin Y Study Com



Solving Trigonometric Equations Ck 12 Foundation
To do this we use the Pythagorean identity sin 2 (A) cos 2 (A) = 1 In this case, we find cos 2 (A) = 1 − sin 2 (A) = 1 − (3/5) 2 = 1 − (9/25) = 16/25 The cosine itself will be plus or minus the square root of 16/25 Which is it?Account Details Login Options Account Management SettingsThe Pythagorean identity tells us that no matter what the value of θ is, sin²θcos²θ is equal to 1 This follows from the Pythagorean theorem, which is why it's called the Pythagorean identity!



Trig Identities And Formulas Pre Calculus Quiz Quizizz



Trigonometric Identities And Examples With Worksheets Math Pictures Identity Precalculus
First one $\tan^2x \sin^2x = (\sin^2 x)(\tan^2 x)$ Tried solving that with the right side but wasn't able to Second one $\csc x / \sec x = \cot x$ I tried solving this one with the left side doing, LS = $\csc x / \sec x $ LS = $(1 / \sin x) / (1 / \cos x) $ LS = $\sin x / \cos x\quad$ (1's cancel out LS = $\tan x$ Don't know what I'm doing wrong here For reference, here is the trig•use these identities in the solution of trigonometric equations Contents 1 Introduction 2 2 Some important identities derived from a rightangled triangle sin2 Acos 2A = 1 sec A = 1tan2 A cosec2A = 1cot2A 2 3 Using the identities to solve equations 4 wwwmathcentreacuk 1 c mathcentre 09 1 Introduction In this unit we are going to look at trigonometric identities and · The trigonometric double angle formulas give a relationship between the basic trigonometric functions applied to twice an angle in terms of trigonometric functions of the angle itself Tips for remembering the following formulas We can substitute the values



Understanding Pythagorean Identities Studypug



Find Sin 2x Cos 2x And Tan 2x If Tan X 1 2 And X Terminates In Quadrant Iii Helpyout
Free math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with stepbystep explanations, just like a math tutorThe subtraction of the tan squared of angle from secant squared of angle is equal to one and it is called as the Pythagorean identity of secant and tangent functions sec 2 θ − tan 2 θ = 1Prove sin^2(theta)cos^2(theta)=1,Prove tan^2(theta)1=sec^2(theta), Prove 1cot^2(theta)=csc^2(theta), Join my fb



Warm Up Prove Sin 2 X Cos 2 X 1 This Is One Of 3 Pythagorean Identities That We Will Be Using In Ch 11 The Other 2 Are 1 Tan 2 X Sec 2 X Ppt Download



Understanding Pythagorean Identities Studypug
Pythagorean identities are identities in trigonometry that are extensions of the Pythagorean theorem The fundamental identity states that for any angle θ, \theta, θ, cos 2 θ sin 2 θ = 1 \cos^2\theta\sin^2\theta=1 cos 2 θ sin 2 θ = 1 Pythagorean identities are useful in simplifying trigonometric expressions, especially in writing expressions as a function of either sinWe can use this identity to solve various problems · Maria plans to use fencing to build an enclosure or enclosures for her two horses A single enclosure would be square shaped and require an area of 2,



9 1 Identities And Proofs Ppt Download
.JPG)


Every Day I M Calculatin I D3 Unit Q Pythagorean Identities
· Proved with negative and Pythagorean identities For the exercises 40, determine whether the identity is true or false If false, find an appropriate equivalent expressionPeriodicity Identities, radians Periodicity Identities, degrees sin (x 2π) = sin xcsc (x 2π) = csc xsin (x 360°) = sin xcsc (x 360°) = csc xcos (x 2πThe Trigonometric Double Angle identities or Trig Double identities actually deals with the double angle of the trigonometric functions For instance, Sin2(α) Cos2(α) Tan2(α) Cosine2(α) Sec2(α) Cot2(α) Double Angle identities are a special case of trig identities where the double angle is obtained by adding 2 different angles In this article, we will cover up



Solved Verify The Identity Tan X Cot X 2 Sec2 X Chegg Com


Trigonometric Identities Mathematics Quiz Quizizz
Sec^2tan^2x 1cot^2x Csc^2x Cot^2 csc^21 THIS SET IS OFTEN IN FOLDERS WITH Reciprocal Identities 6 terms Aspen_McCart Quotient Identities 2 terms Aspen_McCart Even/Odd Identities 6 terms Aspen_McCart Cofunction identities 6 terms Aspen_McCart YOU MIGHT ALSO LIKE Trig Derivatives 23 terms dbouchard92 Reciprocal, Quotient, and Pythagorean IdentitiesProof of the Pythagorean identities The proof of each of those follows from the definitions of the trigonometric functions, Topic 15 Proof of the reciprocal relations By definition sin θ = y r, csc θ = r y Therefore, sin θ is the reciprocal of csc θ sin θ = 1 csc θ where 1over any quantity is the symbol for its reciprocal;The key Pythagorean Trigonometric identity is sin2(t) cos2(t) = 1 tan2(t) 1 = sec2(t) 1 cot2(t) = csc2(t)


Answered Verify The Identity Tan2x Csc2x Bartleby


Precalc Wup 216 Using Trig Identities 2 Simplify
Well, to answer that we need to know in which quadrant A is Since the angle A is between 90 o and 180 o, its sine is positive and its cosine is negative · $3^2 4^2 = 5^2$ Which is true and proves that this identity work To my understanding, that is how this identity work However, when I try to make sense of the $\tan^2x1 = \sec^2x$ and $1\cot^2x=\csc^2x$ identity, using the triangle example from above, it doesn't work For example, here's how I did it on paper,It is seen that `sec^4 x tan^4 x = 1 tan^2 x` is not an identity, instead `sec^4x tan^4x = 1 2*tan^2x` Approved by eNotes Editorial Team We'll help your grades soar Start your 48hour


What Is The Formula Of Tan2x Quora



Online Tutoring Math English Science Tutoring Sat Psat Gmat Toefl Ielts Tutors Homework Help
· Set your main menu in Appearance > Menus Search 4142 Frederick ST, Birmingham B1 3HNLesson 5 of Algebra Similarly for the remainingThe Pythagorean Identities are sin^2xcos^2x=1 tan^2x1=sec^2x cot^2x1=csc^2x Some Pythagorean identities can be rewritten sin^2x=1cos^2x cos^2x=1sin^2x Strategies for proving trigonometric identities Some strategies for proving trigonometric identities are to know the fundamental identities and look for ways to apply them, turn things into terms of sine and
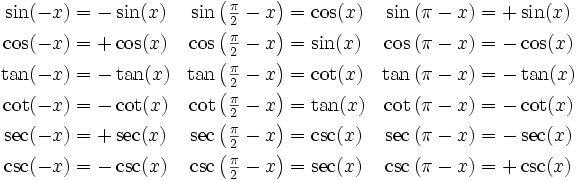


Solvemymath Com Trigonometry Simmetry Shifts Pythagorean Identities



Trigonometric Identity Examples Solutions Videos
Trigonometry Identities Examples and Strategies cosine is an "even" identity; · Use the Pythagorean identities and isolate the squared term 2) Explain how to determine the doubleangle formula for \(\tan(2x)\) using the doubleangle formulas forNotebook Groups Cheat Sheets;



Tangent Half Angle Formula Wikipedia


Derivatives Of Trigonometric Functions
By the Pythagorean Theorem, x^2 y^2 = 1^2 or x^2 y^2 = 1 Approved by eNotes Editorial Team We'll help your grades soar Start your 48hourBecause the two sides have been shown to be equivalent, the equation is an identity tan2(2x)sin2(2x) cos2(2x) = sec2 (2x) tan 2 (2 x) sin 2 (2 x) cos 2 (2 x) = sec 2 (2 x) is an identitySec^4 x tan^2 x = (tan^2x tan^4 x) sec^2 x Answer by MathLover1() (Show Source) use "Pythagorean" identity> identity proven



7 2 47 Integral Of 1 Tan2x Sec2x Cute766



Which Of The Following Is Not An Identity A Cosx Sinx 2 1 2cosx Sinx B 1 Cos 2x Sin 2 1 Brainly Com
· True Start with the well known pythagorean identity sin^2x cos^2x = 1 This is readily derived directly from the definition of the basic trigonometric functions sin and cos and Pythagoras's Theorem Divide both side by cos^2x and we get sin^2x/cos^2x cos^2x/cos^2x = 1/cos^2x tan^2x 1 = sec^2x tan^2x = sec^2x 1 Confirming that the result is an identityIdentities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify Statistics Arithmetic Mean Geometric Mean Quadratic Mean Median Mode Order Minimum Maximum Probability MidRange Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution Physics Mechanics Chemistry



Hello There Get Ready To Flex Math Worksheets 4 Kids Facebook


7 Proving Ids Trig Functions Identities



Trigonometry Reciprocal Identities Expii



Solved Verify The Identity Tan X Cot X 2 Csc 2 X Chegg Com


Biomath Trigonometric Functions


Pythagorean Identities Mathbitsnotebook Ccss Math



Tan 2x Identity Learn Lif Co Id


How Do You Simplify The Identify Sin 2x 1 Cosx 1 Cosx Socratic


Prove The Identity Secxcscx Tanx Cotx 2 Tan 2x Cot 2x1 Apply The Distributive Property2 Apply The Brainly Com



Section 6 3 Double Angle And Half



Warm Up Prove Sin 2 X Cos 2 X 1 This Is One Of 3 Pythagorean Identities That We Will Be Using In Ch 11 The Other 2 Are 1 Tan 2 X Sec 2 X Ppt Download



Warm Up Prove Sin 2 X Cos 2 X 1 This Is One Of 3 Pythagorean Identities That We Will Be Using In Ch 11 The Other 2 Are 1 Tan 2 X Sec 2 X Ppt Download



Is There Any Other Way To Establish This Trig Identity Frac Sec X 1 Tan X Frac Sin X 1 Cos X Mathematics Stack Exchange
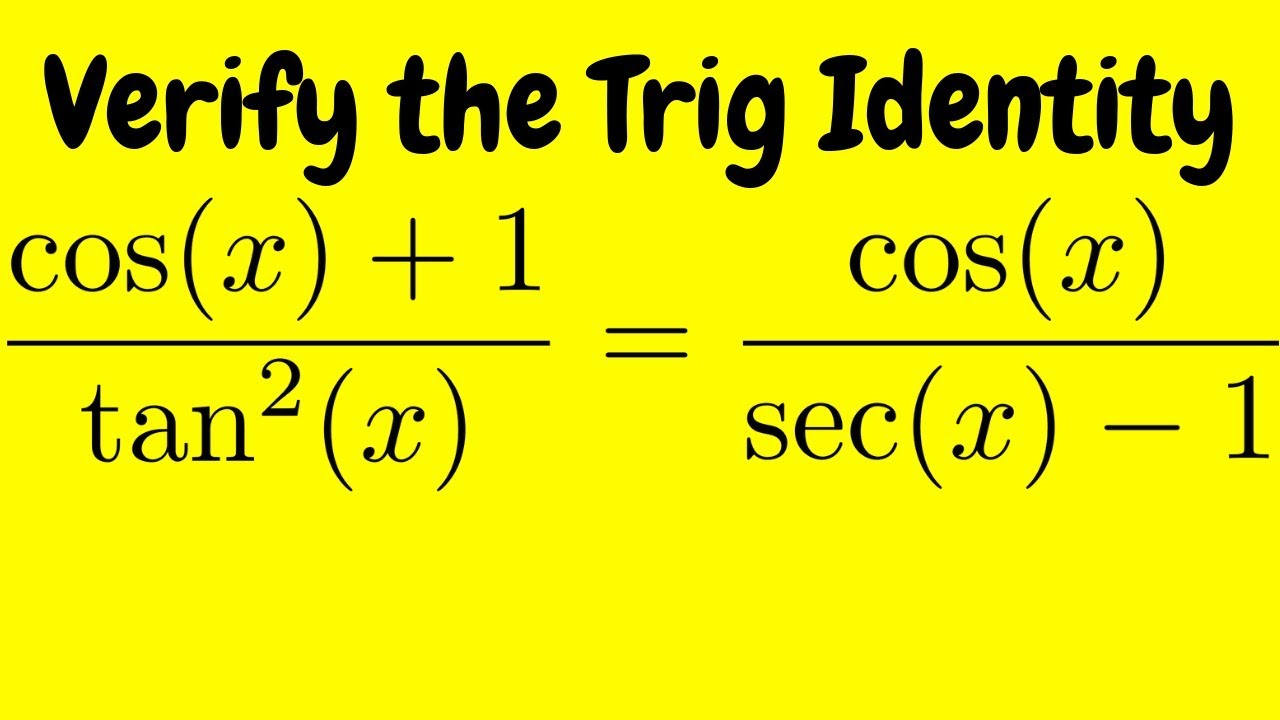


Verifying A Trigonometric Identity Cos X 1 Tan 2 X Cos X Sec X 1 Youtube



Using Double Angle Formulas Objective To Apply The Double Angle



Tan 2x Identity Learn Lif Co Id
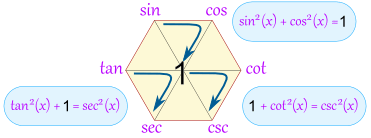


Magic Hexagon For Trig Identities



Trigonometric Identities And Examples With Worksheets


6 1 2 Trigonometric Identities



Answered Power Reducing Formulas Cos 2x 1 Cos Bartleby



List Of Trigonometric Identities Wikipedia



Trig Identity Sec2x Minus Tan2x T10 Youtube



The Young Math Analysis 101 I D 3 Unit Q Pythagorean Identities



Solved Match Expressions In Columns A And B That Complete Chegg Com



Using Trigonometric Identities Video Khan Academy



3 Simplifying Trig Expression 1 Tan 2x Youtube


Biomath Trigonometric Functions



Pythagorean Identities Trigonometry


How Can One Prove That Math Tan 2x 2 Cot X Tan 2x Cot 2 X Math Quora



2sinxcosx Identity Gamers Smart



Trigonometric Identities Simplify Expressions Video Lessons Examples And Solutions


Trigonometric Integrals



How Do You Use The Fundamental Trigonometric Identities To Determine The Simplified Form Of The Expression Socratic



X Y X Y X Y X Y Ppt Download


What Is The Formula Of Tan2x Quora
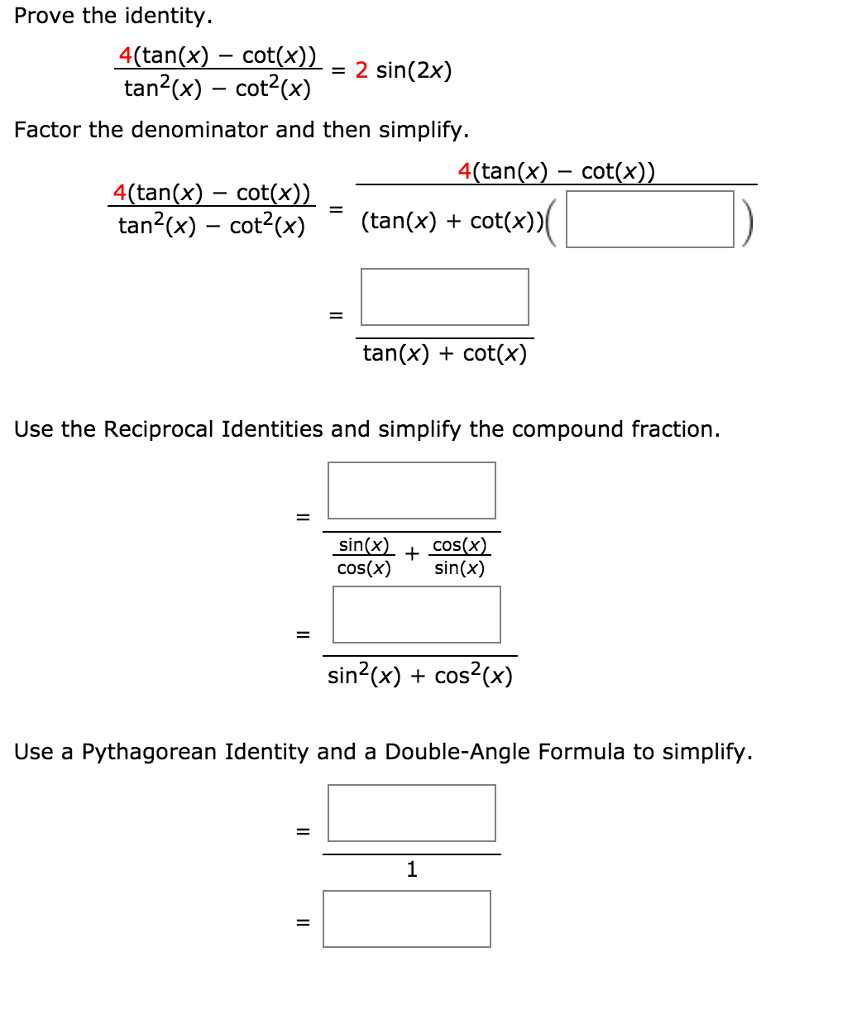


Solved Prove The Identity 4 Tan X Cot X Tan 2 X Chegg Com



The Pythagorean Trigonometric Identity Sin 2 X Cos 2 X 1



Trigonometry Identity Tan 2 X 1 Sec 2 X Youtube
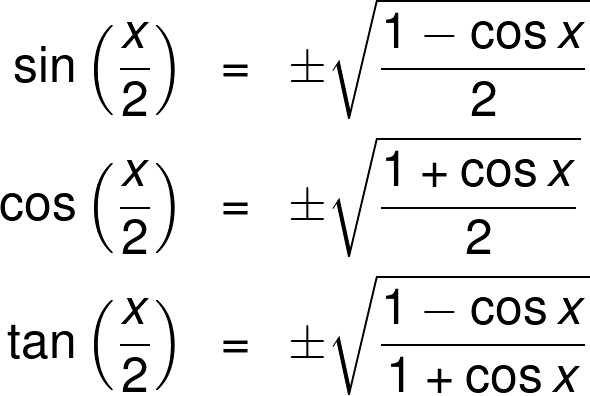


Half Angle Calculator



Integrate Sec 2x Method 2
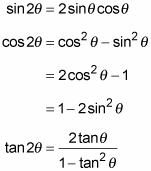


Using The Double Angle Identity For Cosine Dummies



Pythagorean Trigonometric Identity Wikipedia



Trig Identities Calc I



Powers Of Trigonometric Functions



Use Identities To Rewrite Cosx Sinxtanx In Terms Of Sin X And Cos X Then Simplify So That No Quotients Appear Wyzant Ask An Expert
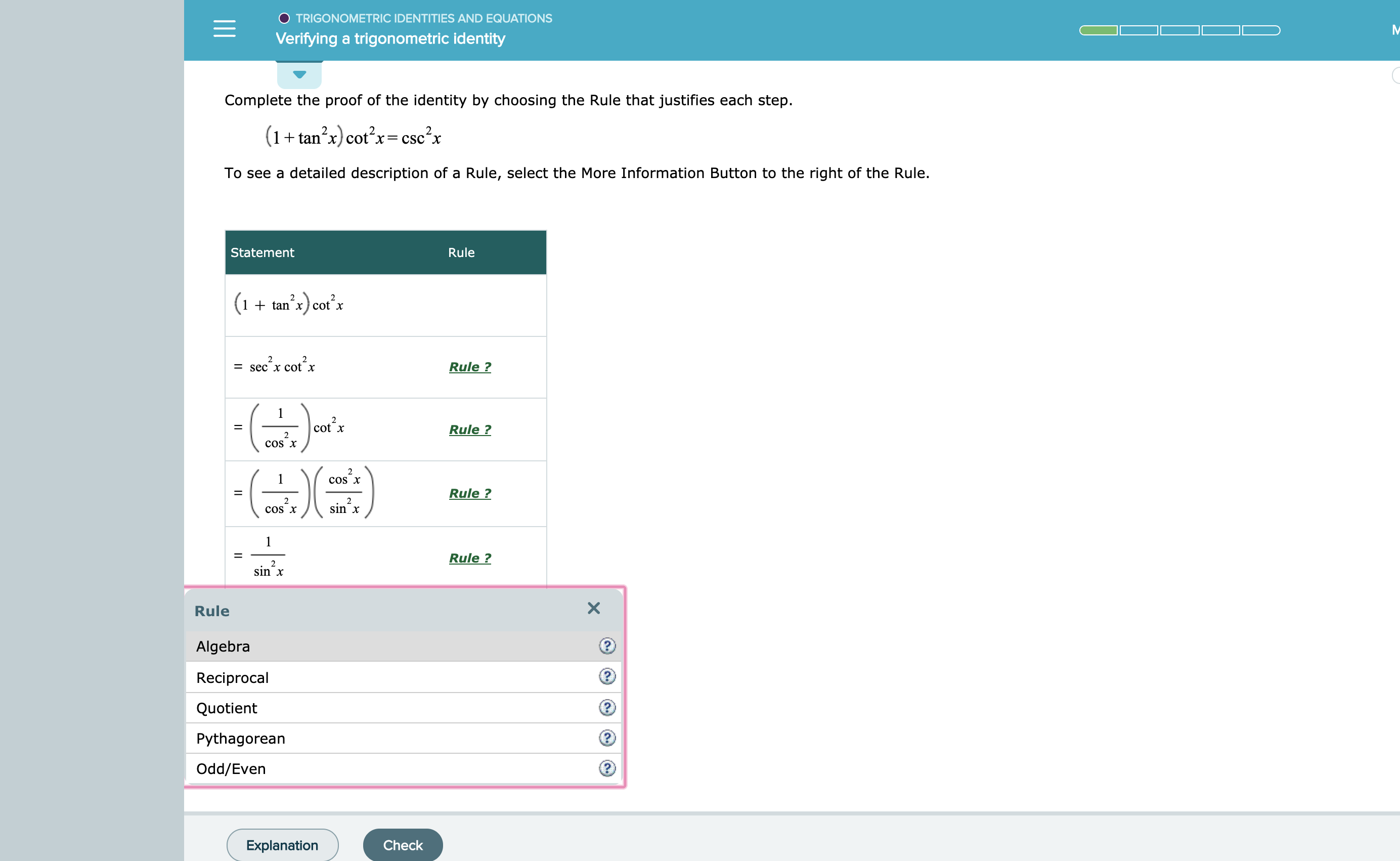


Answered Trigonometric Identities And Equations Bartleby



Derive 1 Tan 2x Sec 2x And 1 Cot 2x Text Cosec 2x Geometrically Mathematics Stack Exchange



7 2 47 Integral Of 1 Tan2x Sec2x Cute766


Solved Cot 0 1 Tan 0 C Even Odd Identity 4 Cot2 0 1 Csc D Quotient Identity 5 Cot 0 Cos Sin 0 6 Sec 0 1 Cos 7 Sec 0 Se Course Hero



Trigonometric Identities Mathandstatshelp


Trigonometry Functions User S Blog



Understanding Pythagorean Identities Studypug



Trig Double Identities Trigonometric Double Angle Functions Trig



Sec 6x Tan 6x 1 2 Tan 2x Sec 2x Important Difficult Trigonometric Identity Youtube



Solved Verify The Identity Cot X Tan X 2 Csc2 X Se Chegg Com



Trigonometric Identity With Pythagorens Sec 2x Sin 2x Cos 2x Tan 2x Youtube



Trigonometry Cheat Sheet


Relating Trigonometric Functions Trigonometry Socratic


Trigonometric Integrals



Answered 3 1 Tanx Tan 2x Sec 2x S Bartleby



Ch Ppt Download



7 1 Notes


What Is The Formula Of Tan2x Quora
x-1=sec(squared)x.jpg)


10 Identity Tan Squared X 1 Sec Squared X Trigonometry Educator Com



1 1 Csc Or Sin Or Csc Sin 1 Sin Csc X X X X X X 1 1 Sec Or Cos Or
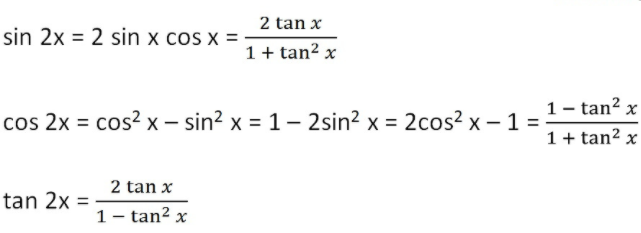


Formula Of Trigonometry Sin Cos Tan Cot Sec Cosec



0 件のコメント:
コメントを投稿